1388. Заправки
В стране есть n городов, некоторые из которых
соединены между собой дорогами. Для того чтобы проехать по одной дороге,
требуется один бак бензина. В каждом городе стоимость полного бака бензина разная. Ваша задача – добраться
из первого города в n-ый с минимальными затратами.
Вход. Первая строка содержит количество городов n (1 ≤ n ≤ 100). Вторая строка содержит n чисел, i-ое из которых
задает стоимость бензина в i-ом
городе (все числа целые, от 0 до 100). Третья строка содержит количество дорог m в стране, за которой идет описание
самих дорог. Каждая дорога задается двумя числами – номерами городов, которые
она соединяет. Все дороги двухсторонние (то есть по ним можно двигаться в обоих
направлениях), между двумя городами существует не более одной дороги, а
также не существует дорог, ведущих из города в себя.
Выход. Выведите одно
число – минимальную стоимость маршрута или -1, если добраться до n-го
города невозможно.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 1 10 2 15 4 1 2 1 3 4 2
4 3 |
3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 1 10 2 15 0 |
-1 |
РЕШЕНИЕ
графы –
алгоритм Дейкстры
Анализ алгоритма
Пусть cost[i] – стоимость бензина в i-ом городе. Для каждой пары городов i и j
проведем ориентированное ребро из i в
j с весом cost[i], а также ориентированное ребро из j в i с весом cost[j].
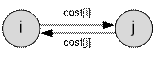
Для решения
задачи следует найти путь минимальной стоимости из города 1 в город n.
Пример
Построим граф,
приведенный в первом примере.
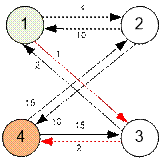
Маршрут минимальной
стоимости из вершины 1 в вершину 4 имеет вид: 1 → 3 → 4. Его
стоимость равна 1 + 2 = 3.
Реализация алгоритма
Граф будем хранить
в матрице смежности g. Текущие
кратчайшие расстояния от начальной вершины 1 до остальных вершин графа
пересчитываем в массиве d. В массиве cost храним стоимость бензина в каждом городе.
#define MAX 110
#define INF 0x3F3F3F3F
int g[MAX][MAX],
used[MAX], d[MAX], cost[MAX];
Читаем количество городов n
и стоимость бензина в каждом из них.
scanf("%d",&n);
for(i = 1; i <= n; i++)
scanf("%d",&cost[i]);
Строим граф стоимостей переездов между городами.
memset(g,0x3F,sizeof(g));
memset(used,0,sizeof(used));
scanf("%d",&m);
for(i = 1; i <= m; i++)
{
scanf("%d
%d",&a,&b);
g[a][b] = cost[a];
g[b][a] = cost[b];
}
Инициализируем кратчайшие расстояния от первой вершины до
остальных.
memset(d,0x3F,sizeof(d));
d[1] = 0;
Запускаем цикл алгоритма Дейкстры. На
каждой итерации находим вершину w с
минимальным расстоянием mind до начальной
вершины.
for(i = 1; i < n; i++)
{
mind = INF; w = -1;
for(j = 1; j
<= n; j++)
if
(!used[j] && d[j] < mind) {mind = d[j]; w = j;}
Если оказалось, что w = -1, то искомого пути не существует,
и мы выходим из цикла.
if (w < 0)
break;
Релаксируем все ребра, исходящие из
вершины w.
for (j = 1; j <= n;
j++)
if (!used[j]) d[j] =
min(d[j], d[w] + g[w][j]);
Кратчайшее расстояние до вершины w вычислено.
used[w] = 1;
}
Выводим ответ в зависимости от
значения dist[n]. Если оно равно
бесконечности, то пути до вершины n
не существует. Иначе выводим искомое кратчайшее расстояние.
if (d[n] == INF) printf("-1\n");
else printf("%d\n",d[n]);
Java реализация
import java.util.*;
public class Main
{
static final int INFINITY = 2000000000;
static int g[][], used[], dist[], cost[];
static void Relax(int i, int j)
{
if (dist[i] + g[i][j] < dist[j])
dist[j] = dist[i] + g[i][j];
}
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
int n = con.nextInt();
g = new int[n+1][n+1];
for (int[] row: g) Arrays.fill(row, INFINITY);
cost = new int[n+1];
for (int i = 1; i <= n; i++)
cost[i] = con.nextInt();
used = new int[n+1]; Arrays.fill(used, 0);
dist = new int[n+1]; Arrays.fill(dist, INFINITY);
dist[1] = 0;
int m = con.nextInt();
for (int i = 1; i <= m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = cost[a];
g[b][a] = cost[b];
}
for (int i = 1; i < n; i++)
{
// find vertex w with minimum d[w] among not used vertices
int min = INFINITY, v = -1;
for (int j = 1; j <= n; j++)
if (used[j] == 0 && dist[j] < min) { min = dist[j]; v = j; }
// no more vertices to add
if (v < 0) break;
// relax all edges outgoing from v
// process edge v -> j
for (int j = 1; j <= n; j++)
if (used[j] == 0 && g[v][j] != -1) Relax(v, j);
// shortest distance to v is found
used[v] = 1;
}
if (dist[n] == INFINITY) System.out.println(-1);
else System.out.println(dist[n]);
con.close();
}
}